債券投資の世界に足を踏み入れると、「利回り」という言葉が頻繁に登場します。特に日本市場での債券利回り計算は、投資家にとって非常に重要です。この記事では、利回りの基本から、単利と複利の違い、そして最終的には債券の最終利回りの計算方法まで、詳しく解説します。さあ、利回りの謎を解き明かしましょう!
債券利回りの基本:知っておくべきこと
債券利回りとは、一言で言えば、投資金額に対する収益率のことです。ここで重要なのは、収益が単に利息だけでなく、購入価格と償還価格の差額も含まれるということです。この収益率を理解することは、投資の成否を決める鍵となります。
利回りの種類:単利と複利の違い
まずは、利回りには大きく分けて二つの種類があります。単利と複利です。単利は、元本に対してのみ利息が付く計算方法で、利息は再投資されません。一方、複利は、受け取った利息も再投資され、さらに利息を生む方法です。この違いを理解することは、長期的な投資戦略を立てる際に非常に重要です。
| 利回りの種類 | 説明 |
|---|---|
| 単利 | 元本のみに利息が付く。 |
| 複利 | 利息も再投資され、利息を生む。 |
日本市場での債券利回り計算方法
日本の債券市場では、利回りの計算において特定の慣習が存在します。ここでは、最も一般的な利付債券の最終利回り(単利ベース)の計算方法を見ていきましょう。
利付債券の最終利回りの計算式
利付債券の最終利回りは、以下の計算式で求められます。
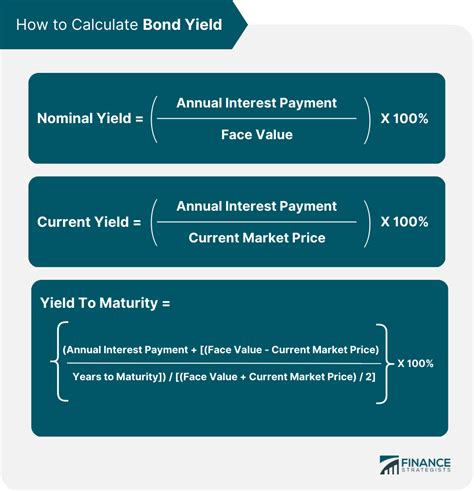
[ \text{最終利回り(%)} = \left[ \frac{\text{年利率} + (\text{償還価格} - \text{買付価格}) ÷ \text{残存年数}}{\text{買付価格}} \right] × 100 ]
この式を使うことで、債券を満期まで保有した場合の収益率を計算することができます。
利回り計算の実例
実際に利回り計算を行うと、どのような結果が得られるのでしょうか。以下の例を見てみましょう。
利回り計算の例
| 項目 | 値 |
|---|---|
| 年利率 | 3% |
| 償還価格 | 100,000円 |
| 買付価格 | 95,000円 |
| 残存年数 | 5年 |
この条件下での最終利回りは、以下のように計算されます。
[ \text{最終利回り(%)} = \left[ \frac{3 + \frac{100,000 - 95,000}{5}}{95,000} \right] × 100 \approx 4.21% ]
この計算結果からわかるように、額面価格よりも安く買った場合、利回りは年利率よりも高くなることがあります。
利回りの計算がもたらす影響
利回りの計算は、単に収益を見積もるためだけのものではありません。投資判断における重要な要素です。例えば、利回りが高ければ高いほど、投資のリスクも高まる可能性があります。ですから、利回りの計算結果を基にリスクを評価し、適切な投資判断を下すことが求められます。
よくある質問
利回りの計算はどのようにして行うのですか?
利回りの計算は、購入価格、償還価格、年利率、残存年数を基に行います。計算式を使って、投資の収益率を算出します。
単利と複利のどちらが良いですか?
それは投資の目的や期間によります。長期的な投資では、複利が有利になることが多いです。
債券利回りが高いほど良いのですか?
必ずしもそうとは限りません。高い利回りは高いリスクを伴うことが多いため、慎重に評価する必要があります。
日本の債券市場と海外の市場では、利回りの計算に違いがありますか?
基本的な計算方法は同じですが、市場の慣習や金利環境により、利回りの水準やリスク評価が異なることがあります。
利回り計算には特別なソフトウェアが必要ですか?
特別なソフトウェアは必要ありませんが、正確な計算を行うために、計算機やスプレッドシートを利用すると便利です。
債券利回りはどのようにして投資判断に影響しますか?
利回りは投資の収益性を示す指標であり、リスク評価や投資戦略の策定に役立ちます。
結論:利回り計算の重要性
債券利回りの計算は、投資の収益性とリスクを評価するための重要な手段です。日本市場における債券利回り計算は、投資家にとって不可欠な知識となります。理解を深め、賢明な投資判断を下すために、この記事を参考にしてみてください。